Category Archives: Tryggingastærðfræði

Að hafa ekki öll eggin í sömu körfu

Að hafa ekki öll eggin í sömu körfu er skýrt og skiljanlegt orðtak um þann ásetning að dreifa áhættu svo að lokaútkoma sé ekki háð einum atburði heldur summu margra. Maður sem gengur eftir götu með eggjakörfur í sitthvorri hendinni kann að auka líkurnar á því að fleiri egg komist ósködduð á áfangastað en hefði hann borið þau öll í sömu körfunni. Myndmálið leynir sér ekki.

Höfuðsetning tölfræðinnar (central limit theorem) lýsir stærðfræðilega hvað gerist þegar við berum einstakar útkomur, sem eru háðar tilviljanakenndum atubrðum, saman við summu útkoma fyrir marga atburði.

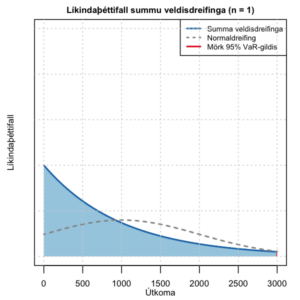
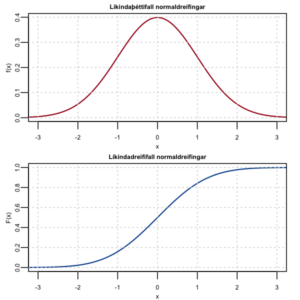
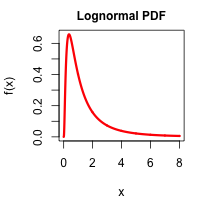
Líkindaþéttifall veldisdreifiðrar slembibreytu og normaldreifðrar slembibreytu með sama meðaltal og staðalfrávik

Blái ferillinn á myndinni til hægri lýsir líkindaþéttifalli veldisdreifðrar slembibreytu, sem hefur meðaltal jafnt 1000. Staðalfrávik slembibreytunnar er jafnt meðaltalinu. Til einföldunar gætum við látið veldisdreifinguna lýsa fjártjóni, sem hlýst af einum tilteknum atburði.

Rauða línan, sem vart má greina yst til hægri, sýnir mörk 95% vágildis (Value-at-Risk, VaR). Það er 2996 og samkvæmt skilgreiningu eru 95 af hverjum 100 tjónum eru undir mörkunum en fimm eru yfir. Hali dreifingarinnar er ekki sýndur en hann teygir sig út í óendanlegt.

Til hliðsjónar er einnig teiknað líkindaþéttifall normaldreifðrar slembibreytu með sama meðaltal og staðalfrávik. Við getum greint toppinn á bjöllulaga forminu, sem oft er kennt við þýska stærðfræðinginn Fredrich Gauss. Halar normaldreifða líkindaþéttifallsins eru utan við bilið, sem myndin spannar.

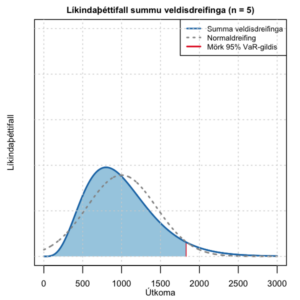
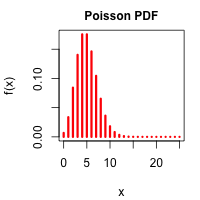
Líkindaþéttifall meðaltals fimm veldisdreifinga (Gamma-dreifingar).

Nú ákveða fimm einstaklingar að deila fjártjóni vegna jafn margra óháðra atburða. Útkomu sérhvers tjóns er lýst með sömu dreifingu og áður. Væntur hlutur sérhvers fimmmenningana í heildartjóninu er eftir sem áður jafn meðaltali hvers fjártjóns en halar dreifingarinnar hafa dregist saman. Líkur á háum útkomum fyrir sérhvern þeirra hefur lækkað og 95% vágildi dreifingarinn er nú um 1830.

Líkindaþéttifallið á myndinni til vinstri lýsir meðaltali fimm veldisdreifinga. Dreifingar með þessari lögun nefnast Gamma-dreifingar. Þá má líka greina að blái ferillinn hefur nálgast líkindaþéttifall normaldreifðu slembibreytunnar, sem lýst er með brotastrikinu. Samkvæmt höfuðsetningu tölfræðinnar stefnir meðaltalið á að vera normaldreifing þegar fjöldi fjártjóna stefnir á óendanlegt.

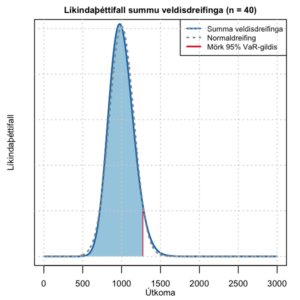
Meðaltal fjörutíu veldisdreifðra slembibreyta.

Allt í veröldinni er af endanlegum fjölda og ekki þarf að leggja saman útkomur óendanlega margra atburða til þess að útkoman verði nálægt því að vera normaldreifð.

Myndin hérna til hægri lýsir samsavarandi dreififalli fyrir meðaltal fjörutíu dreifinga. Hérna liggur ferillinn nánast saman við líkindadreififall normaldreifðu slembibreytunnar. Vert er að geta þess að mörk 5% hæstu mögulegra útkoma hefur enn lækkað.

Hreyfimyndin hér á eftir lýsir líkindadreififalli fyrir meðaltal slembibreyta með breyilegum fjölda. Í upphafi er líkindaþéttifallið eins og fyrsta myndin hér að ofan. Eftir því sem atburðum fjölgar þá þokast meðalútkoman nær normaldreifingunni. Líkur á háum útkomum minnka eftir því sem halar dreifingarinnar dragast saman.

Poisson líkindadreifingin

Í fyrri færslu um líkindadreifingar var fjallað um stakrænar og samfelldar dreifingar. Þar var rakið að í tjónalíkönum má nota stakrænar dreifingar til þess að tákna tíðni tjóna en samfelldar dreifingar til að tákna stærðargráðu hvers tjóns. Útkomur stakrænna dreifinga eru heilar tölur, þ.e. 0, 1, 2, 3, o.s.frv. en útkomur samfelldra dreifinga allar rauntölur. Fyrir tjónalíkön takmörkum við valið við samfelldar dreifingar með útkomur stærri en núll.

Stikar líkindadreifinganna lýsa stærð og lögun líkindadreifi- og líkindaþéttifallanna. Þá sýnir yfirlitið, sem fylgdi í fyrri færslu, ýmsar gagnlegar stærðir hverrar dreifingar, t.d. væntigildi og staðalfrávik. Væntigildi líkindadreifingarinnar lýsir meðalútkomu og staðalfrávik er mælikvarði á frávik frá meðalútkomunni.

Dæmi um stakræna líkindadreifingu er Poisson dreifingin, sem notar stikann $$\lambda$$ (gríska bókstafinn lambda). Stikinn $$\lambda$$ lýsir hvort tveggja meðaltali og ferviki (staðalfráviki í öðru veldi) Poisson dreifingarinnar. Útkomurnar eru heilar tölur stærri en eða jafnar núlli og má nota til þess að tákna fjölda atburða á sérhverju tímabili. Samkvæmt líkindafallinu eru líkur á k atburðum jafnar

$$p_k = \frac{e^{-\lambda} \lambda^k}{k!}$$.

Þ.e.a.s. líkurnar á útkomunni núll og þar með engum atburði eru $$e^{-\lambda}$$, líkur á einum atburði eru $$e^{-\lambda} \lambda$$, líkur á tveimur atburðum eru $$\frac{1}{2}e^{-\lambda} \lambda^2$$, líkur á þremur atburðum eru $$\frac{1}{6}e^{-\lambda} \lambda^3$$, o.s.frv. Mynstrið er þekkt.

Líkindafall Poisson dreifinga

Hugsum okkur dæmi um tryggingafélag, sem flokkar ökumenn þrjá áhættuflokka: lægsta, miðlungs og hæsta. Félagið notar Poisson líkindadreifinguna til þess að tákna tjónatíðni þeirra. Það hefur fundið út að viðskiptavinir í lægsta áhættuflokki valdi að jafnaði 0,1 tjóni á ári pr. ökumann en 0,4 tjón á ári pr. ökumann í miðlungs áhættuflokki og 0,7 tjón að jafnaði í þeim hæsta. Með því að setja stuðlana inn í jöfnurnar fyrir ofan má finna líkindi á fjölda tjóna, sem ökumaður í hverjum flokki veldur. Niðurstaðan er sýnd í meðfylgjandi töflu og líkindafallið er sýnt á myndinni til hægri.

Fjöldi	Áhættuflokkur
tjóna	Lægsti, $$\lambda=0,1$$	Miðlungs, $$\lambda=0,4$$	Hæsti, $$\lambda=0,7$$
0	0.905	0.670	0.497
1	0.090	0.268	0.348
2	0.005	0.054	0.122
3	<0.001	0.007	0.028

Sýni af normaldreifðu slembibreytunni

Í keppni um athygli bjóða fyrirtæki og aðrir aðilar nýjum vinum að tengjast sér í gegnum samfélagsmiðla og heita gjarnan verðlaunum til að örva aðsóknina. Af gamansemi var lofað að draga út milljón sýni af normaldreifðu slembibreytunni þegar Actuary.is næði því marki að eiga yfir eitthundrað vini á Facebook-síðunni. Það var allgóð aðsókn að vefsíðunni þegar frétta- og bloggvefir bentu á umfjöllun um nettó eigna- og skuldastöðu kynslóðanna fyrr í mánuðinum. Margir gerðust vinir síðunnar með því að smella á Like-hnappinn hér uppi til hægri. Vinir síðunnar eru núna orðnir gott betur en eitthundrað. Þeim, sem hafa komið efninu á framfæri við vini og venslafólk, er þökkuð aðstoðin við útbreiðsluna.

Öllu gamni fylgir nokkur alvara og nú er komið að efndum. Af praktískum ástæðum verða sýnin færri en milljón en í stað þess verður spyrt við umjöllunina hvernig þau eru framkölluð.

Eitt sinn var sögð saga frá árdögum tölvuútreikninga við spágerð í veðurfræði, sem kann að hafa byggt á e-s konar hermun. Það fylgdi sögunni að útreikningarnir hefðu krafist mikils reikniafls og veðrið hefði í reynd verið komið löngu á undan spánni. Með tilkomu aukins reikniafls í einkatölvum og tölvuklösum opnast ótal möguleikar. Margir þekkja möguleika með innbyggðum föllum og viðbótarpökkum í Excel töflureikninum. Þá bjóða forritunarmál eins og R-hugbúnaðurinn upp á öfluga hermunartól, sem eru þjál í notkun.

Hermun er notuð ýmsum viðfangsefnum. Í grunninn gengur hermun á því að búa til reikniverk þar sem inntakið eru óþekktar stærðir, sem við þekkjum betur sem slembibreytur. Óþekktu stærðirnar geta lýst hlutfallsbreytingu á virði verðbréfa á einum degi, fjöldi jarðsjálfta á ákveðnu tímabili eða matsfjárhæð skaða í líkams- eða eignatjóni. Einstakar útkomur slembibreytanna eru óþekktar en upplýsingar um mögulegar útkomur eru þekktar eða áætlaðar. Í þessum dæmum getur útkoman, sem við höfum áhuga á, lýst virði kaupréttar á verðbréf eða væntigildi bóta til þess sem kaupir sér tryggingu fyrir fjárskaða vegna tjóns.

Líkindafall og líkindadreififall fyrir útkomur sex hliða tengings.

Slembibreytum er lýst með líkinda-, líkindadreifi- og líkindaþéttiföllum. Einfalt dæmi er útkoman þegar sex hliða tengini er kastað. Líkindafallið táknar líkur á hverri og einni útkomu en líkindaþéttifallið táknar líkur þess að útkoman sé minni en eða jafnt og tiltekið gildi. Líkindafall og líkindaþéttifall fyrir útkomur fullkomins sex hliða tenings er sýnt á myndinni til hægri. Útkoma teningsins er dæmi um stakræna slembibreytu. Út úr líkindafallinu á efri myndinni getum við lesið að líkur á hverri og einni útkomu eru 1/6, gjarnan táknað sem 0,1667 eða 16,67%. Af neðri myndinni má lesa líkindi þess að útkoman sé lægri en eða jöfn tölunni á lárétta ásnum. Þannig eru líkurnar 0,50 eða 50% að útkoman sé lægri en eða jöfn tölunni 3 (þ.e.a.s. að útkoman sé 1, 2 eða 3).

Líkindadreififall og líkindaþéttifall normaldreifingar.

Samfelldum slembibreytum er lýst á áþekkan hátt og myndirnar til vinstri sýna líkindadreifi- og líkindaþéttifall normaldreifðu slembibreytunnar með meðaltal núll og einingastaðalfrávik. Til þess að finna líkur þess að útkoma sé að ákveðnu bili má reikna flatarmálið undir ferlinum innan þess bils. Líkur á einni einstakri útkomu eru núll. Að sama skapi sést að líkindadreififall normaldreifðu slembibreytunnar er ekki þreplaga líkt og dreififallið fyrir fullkomna teninginn. Við getum lesið af lóðrétta ás líkindadreififallsins líkur þess útkoma slembibreytunnar sé lægri eða jöfn gildinu á lárétta ásnum.

Notkun líkindadreififallsins er grunnurinn að þeirri hermunaraðferð, sem lagt er upp með hér og nefnist aðferð andhverfrar vörpunar (inverse method). Hana má nota þegar líkindadreififallið er andhverfanlegt. Aðferðin gengur út á að safna fyrst sýnum jafdreifðu slembibreytunnar og varpa þeim síðan yfir dreifinguna, sem sóst er eftir.

Hreyfimyndin hér fyrir neðan sýnir hermun tíu þúsund sýna af normaldreifðu slembibreytunni á myndrænan hátt. Við getum ímyndað okkur að fyrst rigni niður tíu þúsund sýnum, sem eru jafndreifð á bilinu 0 til 1 og við táknum það með bláu punktunum. Næst vörpum við þeim sýnum niður á talnalínu normaldreifingarinnar með því að finna skurðpunkt líkindadreififallsins við láréttra línu frá sérhverju sýni. Frá skurðpunktinum drögum við lóðrétta línu niður á talnalínu normaldreifingarinnar. Eftir vörpunina má sjá að dreifing sýnanna fellur vel að líkindaþéttifalli normaldreifingarinnar.

English summary:

Above you will find brief discussion about probability functions, probability density functions and probability distribution functions for random variables. As an example both probability function and probability distribution function are drawn for perfect dice to represent an arbitrary discrete random variable. As well, you will recognize the probability density function and probability distribution function for the normal random variable as example of frequently used discrete random variable.

The purpose of this post is to simulate ten thousand samples from the normal distribution using the inverse method. In the beginning, ten thousand samples from the uniform distribution are generated using random number generator within the R software package. Samples from the uniform distribution are represented with blue dots in the animated picture above. Each sample is transformed using the inverse of the normal probability distribution function. As the red samples stack up on top of previous samples we can recognize the shape of our imaginary pile of random numbers approximates the bell shaped probability density function for the normal random variable.

Aldurspíramíti

Aldurspíramítar eru notaðir til þess að sýna aldursskiptingu þjóða. Hreyfimyndin hér fyrir neðan sýnir aldursskiptingu Íslendinga árlega frá 1841 til 2012 m.v. hvert fimm ára aldursbil. Upplýsingarnar eru fengnar frá Hagstofu Íslands. Bláu súlurnar til vinstri tákna fjölda karlmanna í hverju aldursbili og rauðu súlurnar til hægri lýsa fjölda kvenna. Eins og greina má hefur aldurssamsetning þjóðarinnar breyst verulega á tímabilinu.

Myndin hér fyrir neðan sýnir hlutfallsskiptingu hvers árs. Í upphafi tímabilsins er píramítinn þríhyrningslaga, þ.e. fjöldi einstaklinga í hverju bili lækkar með hækkandi aldri. Raunar má segja að sú lögun hafi nokkurn vegin haldist frá 1841 og þar til um 1950 er fæðingartíðni jókst verulega. Eftir 1970 lækkaði fæðingartíðni aftur og hefur staðið nokkuð jöfn frá því um miðjan níunda áratug síðustu aldar. Í dag munar ekki miklu á yngstu ellefu aldurshópunum, þ.e. fjölda þeirra sem falla í hvert fimm ára aldursbil frá nýburum til 55 ára aldurs.

Áhugasamir geta stoppað myndirnar með því að hægrismella á þær og taka hakið úr Play eða hindra endurtekningu með því að taka hakið úr Loop.

Hækkun lífeyrisaldurs

Í þessari frétt á mbl.is frá því í síðustu viku er greint í mjög stuttu máli frá hugmynd nefndar um jöfnun lífeyrisréttinda um hækkun lífeyrisaldurs úr 67 ár í 70. Þá er greint frá því að nefndin sé að skoða hvaða möguleikar séu færir til þess að lífeyrissjóðir geti greitt sem nemur 76% af ævitekjum til þess, sem greiðir í 40 ár í lífeyrissjóð. Í ljósi þess er áhugavert að skoða þróun lífslíkna Íslendinga síðustu áratugina og hvaða áhrif lengri lífaldur hefur á iðgjaldagreiðslur miðað við óbreyttan lífeyrisaldur.

Þróun lífslíkna karla og kvenna 1971-2010

Þróun lífslíkna karla og kvenna 1971 til 2010. Heimild: Hagstofa Íslands

Myndin hérna til hægri byggir á gögnum frá Hagstofu Íslands og sýnir lífslíkur karla og kvenna á hverju fimm ára tímabili frá 1971 til 2010. Ferlarnir tákna hlutfall eftirlifenda á hverjum aldri (survival function) miðað við þá sem fæddir voru. Í byrjun er 100% mannfjöldans á lífi en þeim fækkar eftir því sem líður á. Við 100 ára aldur eru fáir eftirlifendur.

Ljósu ferlarnir svara til fyrstu tímabilanna en síðari tímabil eru teiknuð með dekkri línunum.

Þessi gögn eru notuð til þess að meta núvirði greiðslna, sem sjóðsfélagi greiðir í lífeyrissjóð, sem og núvirði væntra lífeyrisgreiðslna. Þær upplýsingar eru notaðar til þess að ákvarða iðgjald lífeyristryggingarinnar sem hlutfall af launum. Eins og lýst er í fréttinni er gengið út frá því að sjóðsfélagar greiði iðgjöld frá 27 ára aldri til 67 ára aldurs eða á meðan þeir er á lífi. Þeir sem ná að hefja töku lífeyris þiggja 76% af launum til æviloka. Hér er einungis verið að bera saman áhrif hækkaðs lífaldurs og því ekki gert ráð fyrir öðrum þáttum, s.s. örorkubótum, launabreytingum á starfsævinni eða kostnaði við rekstur kerfisins.

Iðgjald lífeyristrygginga 1971-2010 sem hlutfall af launum m.v. að greitt sé frá 27 ára aldri til 67 ára þegar taka lífeyris hefst. Lífeyrisgreiðslur eru 76% af launum.

Myndin til vinstri sýnir iðgjald sem hlutfall af launum miðað við lífslíkur karla og kvenna á hverju tímabili. Verð lífeyristryggingar er reiknað sem hlutfall núvirðis lífeyrisgreiðslna deilt með núvirði iðgjalda. Sökum væntinga um lengri ævi er hlutfallið hærra fyrir konur en karla. Ljóst er að hækkaður lífaldur kallar á hækkun iðgjalda til að tryggja óbreytt hlutfall lífeyrisgreiðslna. Árin 1971-1975 hefðu iðgjöld karla átt að vera 7,5% launa samanborið við 10% á árunum 2005-2010. Hjá konum hefði hlutfallið þurft að vera 9,5% í byrjun en 11,3% í lokin.

Gera verður fyrirvara um að þessir útreikningar byggja á dánarlíkum hvers árabils en ekki spá um dánarlíkur í framtíðinni. Ennfremur er rétt að hnykkja á þeim fyrirvara að útreikningarnir taka ekki tekið tillit til annarra bóta, sem greiddar eru úr samtryggingarkerfinu, eða rekstrarkostnaðar.

Safn líkindadreifinga

Meðfylgjandi er að finna yfirlit yfir nokkrar gagnlegar líkindadreifingar, sem nota má í tjónalíkönum. Meira verður fjallað um líkindadreifingar síðar en þær skiptast í tvo hópa; stakrænar og samfelldar en þær geta einnig verið blanda af hvoru. Í skjalinu má finna margar gagnlegar stærðir sem lýsa dreifingunum, s.s. meðaltal, og fervik. Þá fylgir listi yfir föll í forritunarmálinu R sem nota má til þess að herma sýni af sérhverri dreifingu.

Sýni stakrænna líkindadreifinga geta aðeins verið heilar tölur og þær má nota til að tákna tíðni atvika, s.s. fjölda árekstra sem ökumaður lendir í á einu ári o.s.frv. Dæmi um stakræna líkindadreifingu er Poisson dreifingin og líkindaþéttifall (líkindafall) dreifingarinnar er sýnt hér til hægri. Stærð hverrar súlu táknar líkur á tilsvarandi útkomu.

Samfelldar líkindadreifingar geta tekið tekið óendanlega mörg gildi á bilinu, sem myndmengi þeirra spannar. Í tjónum er skaðinn alltaf stærri en núll, líkt og líkja má eftir með lognormal líkindadreifingunni hérna til vinstri. Hægt er að reikna líkur þess að útkoman sé á tilteknu bili með því að reikna flatarmálið undir ferlinum innan þess svæðis sem við á.

English summary: Attached is a list of frequently used probability distributions in loss models.

Notkun R forritunarmálsins

Þeir sem þekkja til R forritunarmálsins vita að það er eftir ýmsu því tengdu að slæðast á netinu. Síðustu árin hefur verið veldisvöxtur í fjölda pakka, sem notendur geta nálgast frítt. Bæði byrjendur og lengra komnir geta haft gagn og gaman af þessari kynningu Jim Guszcza á notkun R í ýmsum viðfangsefnum tengdum tryggingastærðfræði. Það er vel þess virði að horfa á.

Ég kynntist Jim síðasta vetur þegar hann var prófessor í tryggingastærðfræði við University of Wisconsin-Madison þar sem ég tók námskeið hjá honum. Þar byrjaði ég að nota R í fyrsta sinn sem bætti miklu við hagnýtingu námsefnisins.

Those who are familiar with the R programming language know the near endless resources available online. In recent years, the number of free libraries has grown exponentially. Beginners and advanced programmers can enjoy and learn from this presentation given by Jim Guszcza on actuarial applications using R. I guarantee it is worth watching.

It was my privilege to sit Jim’s class on loss models during my studies at the University of Wisconsin-Madison last year. His extensive use of R added a lot to the practical aspects of the course material.

httpv://www.youtube.com/watch?v=yWexhOmkVKU

Lífslíkur

Forsenda þess að verðleggja líftengdar tryggingarafurðir, hvort heldur er líftryggingar eða lífeyriseign, er að meta lífslíkur einstaklings, sem í hlut á. Það er því við hæfi að fyrsta efnilega innleggið í þessu bloggi fjalli um mat á lífslíkum.

Til þess að meta lífslíkur er stuðst við upplýsingar um mannfjölda og andlát. Í mannfjöldatöflum er alla jafna skráð hve mörg heil ár einstaklingar lifa. Út frá upplýsingum um mannfjölda og andlát fyrir hvert aldursbil má reikna lífslíkur hvers aldursárs. Að því gefnu er svo hægt að reikna ólifaða meðalævi, þ.e. fjölda ára sem einstaklingur getur vænst þess að lifa að því gefnu að hann sé á lífi við tiltekinn aldur.

Myndin hér fyrir neðan sýnir lífslíkur nýbura á Íslandi m.v. dánartíðni árið 2011 skv. tölum um mannfjölda og andlát, sem Hagstofa Íslands skráir. Heilu línurnar tákna lífslíkurnar en brotastrikin tákna 95% öryggismörk. Myndin byggir aðeins á tölum eins árs. Í litlum þjóðfélögum má nota upplýsingar yfir lengra tímabil til þess að minnka óvissubilið.

Samkvæmt myndinni teljast 99,4% líkur á því að nýfætt sveinbarn nái 20 ára aldri og 99,7% líkur á því að stúlkubarn nái sama aldri. Það eru 3,2% líkur á því að karlmaður deyji fyrir fimmtugt en 1,5% að það sama hendi konu.

Í samanburði á milli þjóða er venja að bera saman vænta ævilengd nýbura en á sama hátt má reikna vænta ólifaða meðalævi m.v. hvert aldursár. Þannig má vænta að nýfætt sveinbarn nái um 80 ára aldri og stúlkubörn um 84 ára aldri.

Myndin hér að ofan sýnir væntingar um ólifaða meðalævi fyrir öll aldursár. Nái karlmaður 80 ára aldri er væntur árafjöldi, sem hann á eftir ólifaða, u.þ.b. 8 ár. Kona, sem nær sama aldri, á um 10 ár eftir ólifuð að meðaltali.

Nýtt blogg

Þetta er fyrsta færslan í nýju bloggi um tryggingastærðfræði. Það er ásetningur að fjalla um fræðin á bak við trygginga- og lífeyrismál og flétta saman við málefni líðandi stundar þar sem við á. Ef síðan verður til þess að auka áhuga einhvers á faginu eða varpa upp nýjum vinklum í umræðunni þá er tilganginum náð.

Ég lauk nýverið námi við tryggingastærðfræðideild University of Wisconsin í Madison, Wisconsin í Bandaríkjunum. Áður lauk ég meistaraprófi í rafmagns- og tölvuverkfræði frá Háskóla Íslands.

Jón Ævar Pálmason

Hagur

tryggingastærðfræði og slembin innskot