Í fyrri færslu var fjallað um nýútkomnar auglýsingar Samtaka atvinnulífsins um verðlag, laun og kaupmátt á Íslandi og samanburð þeirra við hin Norðurlöndin. Það er ástæðulaust að endurtaka of mikið af því sem þar kom fram en hér verður lagst í samanburð við eitt landanna; Svíþjóð.
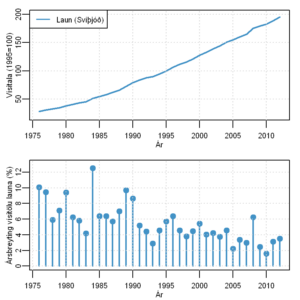
Laun í Svíþjóð (efri) og ársbreyting þeirra (neðri). Heimild: Statistiska Centralbyrån.
Á vef Hagstofu Svíþjóðar, Statistiska Centralbyrån, scb.se, eru til samfelldar skráningar um laun fyrir fullt starf í iðnaðar- og framleiðslustörfum á almennum vinnumarkaði. Þau ná aftur til 1975 og ættu að vera ágæt nálgun á launaþróun í Svíþjóð í samanburði við launavísitölu Hagstofu Íslands.
Í tvo áratugi frá 1975 hækkuðu laun í Svíþjóð að meðaltali um 7,5 prósent að meðaltali á ári en eftir það hafa þau hækkað um 4,0 prósent að jafnaði. Launaþróuninni er lýst á myndinni hér til hægri þar sem gildið hefur verið stillt við 100 árið 1995. Neðra ritið sýnir árlegar hlutfallsbreytingar.
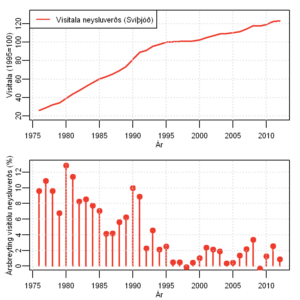
Vísitala neysluverðs í Svíþjóð (efri) og árleg hlutfallsbreyting (neðri). Heimild: Statistiska Centralbyrån.
Hagstofa Svíþjóðar mælir vísitölu neysluverðs eins og sú íslenska. Á línuritinu hérna til vinstri má sjá þróunina frá 1975. Sem fyrr lýsir efri myndin vísitölunni og sú neðri táknar hlutfallsbreytingu frá fyrra ári á hverjum tíma.
Á tímabilinu frá 1975 til 1995 mældist meðalverðbólga í Svíþjóð 7,5%. Fimm af fyrstu tíu árunum mældist verðbólga yfir 10%. Eftir 1995 hefur verðbólga í Svíþjóð verið um 1,3% að meðaltali á ári.
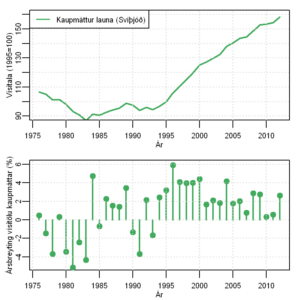
Þróun kaupmáttar launa í Svíþjóð (efri) og árleg hlutfallsbreyting (neðri). Heimild: Statistiska Centralbyrån.
Þrátt fyrir verulegar launahækkanir á fyrri hluta tímabilsins héldu þær ekki í við verðlag svo að það dró úr kaupmætti nær samfellt í tíu ár. Samkvæmt línuritinu var kaupmáttur lægstur árið 1983 og hafði þá lækkað um átján prósent á átta árum.
Í áratug frá 1983 til 1993 jókst kaupmáttur samtals um tæplega níu prósent en hafði þó ekki náð fyrra gildi. Öll ár frá 1993 hefur kaupmáttur launa í Svíþjóð aukist samkvæmt þessum gögnum.
Til þess að skoða þróunina á Íslandi og í Svíþjóð í samhengi hafa vísitölur neysluverðs og launa verið teiknaðar á eina mynd, sem sýnd er hér á eftir. Allar mætast þær í gildinu 100 árið 1995.
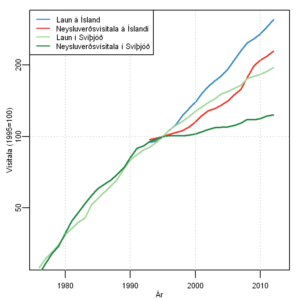
Þróun launa og verðlags á Íslandi og í Svíþjóð. Heimildir: Hagstofa Íslands og Statistiska Centralbyrån.
Eins og fram kom í fyrri færslu jókst kaupmáttur launa á Íslandi öll ár frá 1995 til 2007. Á þessum tíma hækkuðu laun á Íslandi um 130% sé miðað við launavísitölu Hagstofu Íslands og verðlag hækkaði um 58%. Það jafngildir 45% kaupmáttaraukningu.
Á sama árabili hækkuðu laun í Svíþjóð um 65% samkvæmt gögnum sænsku stofnunarinnar en verðlag um 14%. Það skilaði jafn mikilli kaupmáttaraukningu eða 45%! Síðan þá hefur kaupmáttur launa í Svíþjóð vaxið um 10% en dregist saman um 9% á Íslandi.
Áhrif launahækkana
Í síðustu færslu var sýnt samband launahækkana og kaupmáttaraukningar. Ef til vill hefði mátt orða niðurstöðurnar skýrar en greina mátti að háar launahækkanir drógu úr kaupmætti til lengri tíma. Þar var nefnt að mörk hækkana gætu legið á bilinu fjögur til sex prósent. Hækki laun umfram það er líklegt að það hafi neikvæð áhrif á kaupmátt til lengri tíma.
Sér í lagi mátti greina þau áhrif á öðru og þriðja ári eftir mikla hækkun launa. Þetta rímar ágætlega við lögmál í hagfræði um að launahækkanir umfram framleiðniaukningu leiði til aukinnar verðbólgu, sem dregur úr kaupmætti.
Fyrri greining byggði aðeins á gögnum frá Íslandi yfir tveggja áratuga tímabil en með því að bæta við gögnum frá Svíþjóð yfir lengra tímabili lætur nærri að gagnamengið þrefaldist. Það bætir matið á áhrifum þessa sambands, ef rétt reynist.
Myndin hér fyrir neðan sýnir samband launahækkana og breytingar á kaupmætti í báðum löndum fyrir öll skráð ár. Efst til vinstri er sýnt samband launahækkana og kaupmáttaraukningar á því ári sem hún fellur til. Myndin efst til hægri sýnir breytingu kaupmáttar miðað við launabreytingu fyrra árs. Neðri myndirnar sýna breytingarnar tveimur og þremur árum eftir að laun hækka.
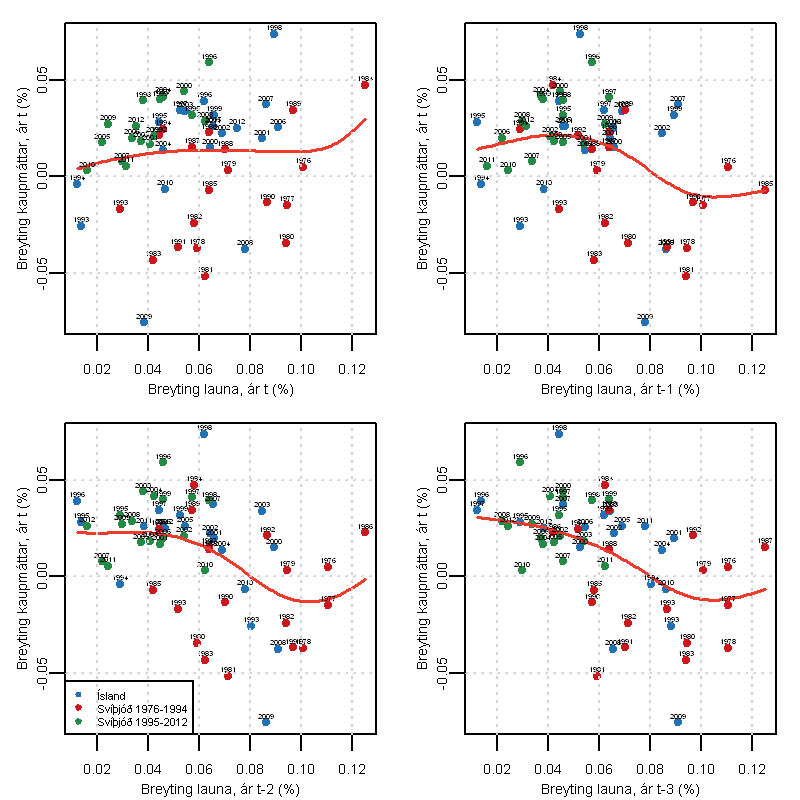
Samband breytinga á vísitölu launa og vísitölu kaupmáttar. Efri myndin til vinstri lýsir sambandi kaupmáttar sama ár og launabreyting. Myndin uppi til hægri lýsir breytingu kaupmáttar og launabreytingar ári áður. Myndirnar í neðri röð lýsa breytingu kaupmáttar tveimur og þremur árum síðar. Heimild: Hagstofa Íslands og Statistiska centralbyrån..
Bláu punktarnir lýsa sambandi launahækkana og kaupmáttar á Íslandi. Rauðu punktarnir lýsa sambandinu í Svíþjóð fyrir árið 1995 og grænu punktarnir 1996 og síðar. Á þremur síðasttöldu myndunum má sjá að fylgnin er neikvæð fyrir mikla hækkun launa. Það kann að vera matsatriði hvar þjálguðu (smoothed) ferlarnir byrja að sveigja niður á við. Álykta má að það geti verið við 4-6% mörkin.
Áhrif gengisbreytinga
Áhrif breytinga á gengi gjaldmiðils má skoða með sama hætti. Hér er miðað við krossgengi íslensku og sænsku krónunnar gagnvart Bandaríkjadal og breytingu frá einu ári til annars. Breytingar á gengi íslensku krónunnar hafa meiri áhrif á verðlag á Íslandi en gengi sænsku krónunnar hefur á verðlag í Svíþjóð.
Myndirnar hér fyrir neðan sýna samband kaupmáttarbreytinga og gengissveiflna milli ára. Efst til vinstri eru sýnd áhrif gengisbreytinga á kaupmátt sama ár og gengisbreyting á sér stað. Næsta mynd sýnir áhrif á kaupmátt ári síðar og svo koll af kolli.
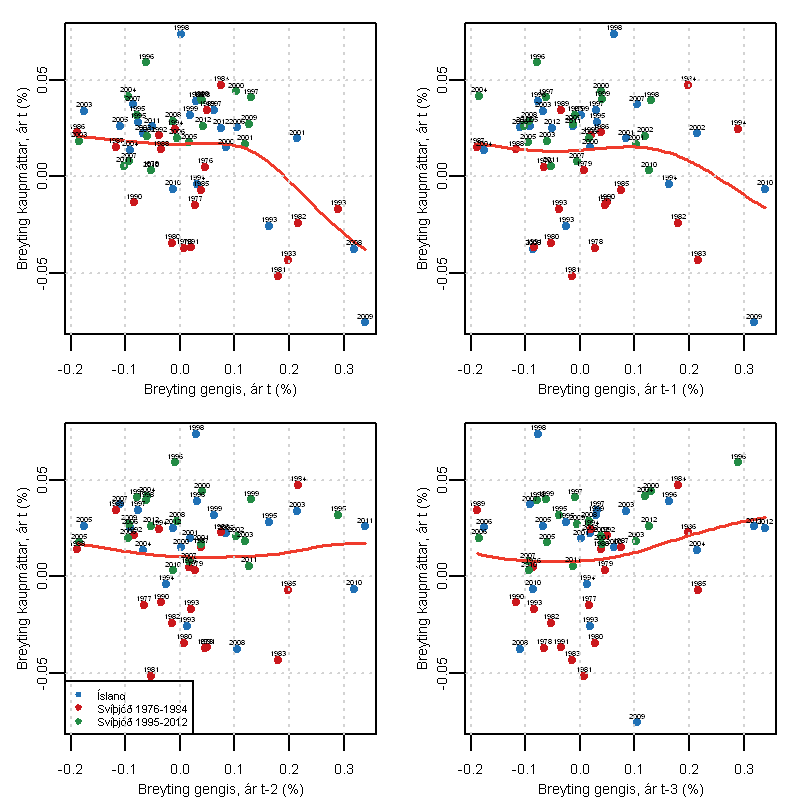
Samband breytinga á gengi gjaldmiðils og kaupmáttar. Efri myndin til vinstri lýsir sambandi kaupmáttar sama ár og launabreyting. Myndin uppi til hægri lýsir breytingu kaupmáttar og launabreytingar ári áður. Myndirnar í neðri röð lýsa breytingu kaupmáttar tveimur og þremur árum síðar. Heimildir: Hagstofa Íslands og Hagstofa Svíþjóðar.
Augljóst er að mikil gengislækkun hefur áhrif á kaupmátt. Þ.e. falli gengi gjaldmiðilsins umfram 10% þá er fylgnin neikvæð. Áhrifin koma fram sama ár og að litlum hluta ári síðar. Áhugavert er að áhrifin eru ekki samhverf, þ.e. styrkist gengi gjaldmiðilsins umfram 10% þá eykur það ekki kaupmátt í jafn miklum mæli gengisfall dregur úr honum hann.
Líkan
Þessar ályktanir eru notaðar til þess að stilla upp línulegu aðhvarfsgreiningarlíkani, sem metur áhrif launahækkana og gengisbreytinga á kaupmátt. Frumbreytur líkansins eru:
- Launahækkanir
- Launahækkanir umfram 5% (án tímahliðrunar og með tímahliðrun)
- Gengisbreytingar umfram 10% (án tímahliðrunar og með tímahliðrun)
Í stuttu máli benda stuðlar endanlegs líkans til eftirfarandi niðurstöðu (marktækni stuðla er táknuð með merkingum innan sviga):
- Hækkun launa: hvert prósent skilar 0,65% aukningu kaupmáttar (*)
- Hækkun launa umfram 5%: hvert prósent dregur úr kaupmætti
- -0,29% á upphafsári
- -0,63% á fyrsta ári (***)
- -0,21% á öðru ári
- -0,42% á þriðja ári (**)
- Samtals -1,55% á fjórum árum.
- Gengisfall umfram 10%: hvert prósent rýrir kaupmátt um 0,22% (***).
Samkvæmt þessu einfaldaða líkani yrði ábati af 2% launahækkun 1,3% aukning kaupmáttar. Fimm prósent launahækkun gæti að skilað 3,25% kaupmáttaraukningu. Hækki laun umfram það rýrnar kaupmáttur til lengri tíma. Til dæmis mætti áætla að hækki laun um 7% þá leiddi það aðeins til 1,45% varanlegrar kaupmáttaraukningar.
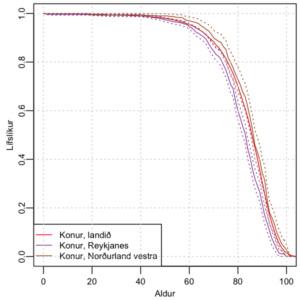
 Í gær kom út nýtt eintak Fjármála, vefrits Fjármálaeftirlitsins. Meðal efnis að þessu sinni er umfjöllun síðuhöfundar um áhrif nýrra líftaflna á skuldbindingar lífeyrissjóða. Þá er grein um fyrirhugaðar breytingar á löggjöf um vátryggingamarkaði eftir Sigurð Frey Jónatansson, tryggingastærðfræðing. Frétt Fjármálaeftirlitsins um útgáfuna má finna hér.
Í gær kom út nýtt eintak Fjármála, vefrits Fjármálaeftirlitsins. Meðal efnis að þessu sinni er umfjöllun síðuhöfundar um áhrif nýrra líftaflna á skuldbindingar lífeyrissjóða. Þá er grein um fyrirhugaðar breytingar á löggjöf um vátryggingamarkaði eftir Sigurð Frey Jónatansson, tryggingastærðfræðing. Frétt Fjármálaeftirlitsins um útgáfuna má finna hér.
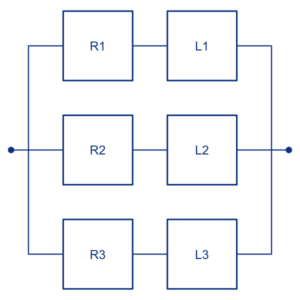
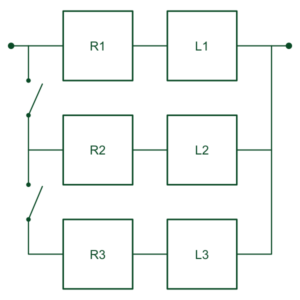
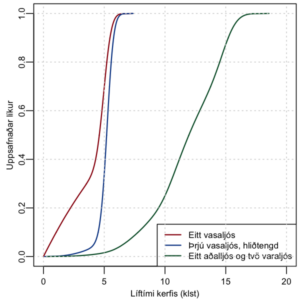
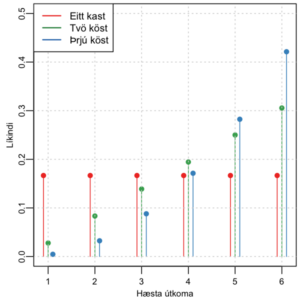
 Vefurinn
Vefurinn 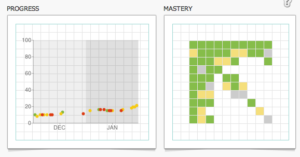
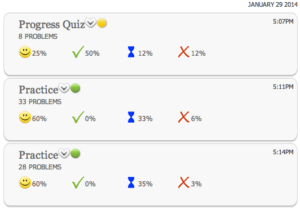 Í viðmóti foreldra og kennara er hægt að fylgjast með framgangi nemanda og sjá niðurbrot á árangri í sérhverri lotu. Þegar nemanda verður tamt að svara dæmum, sem liggja fyrir hverju sinni, er þyngri spurningum bætt við.
Í viðmóti foreldra og kennara er hægt að fylgjast með framgangi nemanda og sjá niðurbrot á árangri í sérhverri lotu. Þegar nemanda verður tamt að svara dæmum, sem liggja fyrir hverju sinni, er þyngri spurningum bætt við.





