Í fyrri færslu um líkindadreifingar var fjallað um stakrænar og samfelldar dreifingar. Þar var rakið að í tjónalíkönum má nota stakrænar dreifingar til þess að tákna tíðni tjóna en samfelldar dreifingar til að tákna stærðargráðu hvers tjóns. Útkomur stakrænna dreifinga eru heilar tölur, þ.e. 0, 1, 2, 3, o.s.frv. en útkomur samfelldra dreifinga allar rauntölur. Fyrir tjónalíkön takmörkum við valið við samfelldar dreifingar með útkomur stærri en núll.
Stikar líkindadreifinganna lýsa stærð og lögun líkindadreifi- og líkindaþéttifallanna. Þá sýnir yfirlitið, sem fylgdi í fyrri færslu, ýmsar gagnlegar stærðir hverrar dreifingar, t.d. væntigildi og staðalfrávik. Væntigildi líkindadreifingarinnar lýsir meðalútkomu og staðalfrávik er mælikvarði á frávik frá meðalútkomunni.
Dæmi um stakræna líkindadreifingu er Poisson dreifingin, sem notar stikann $$\lambda$$ (gríska bókstafinn lambda). Stikinn $$\lambda$$ lýsir hvort tveggja meðaltali og ferviki (staðalfráviki í öðru veldi) Poisson dreifingarinnar. Útkomurnar eru heilar tölur stærri en eða jafnar núlli og má nota til þess að tákna fjölda atburða á sérhverju tímabili. Samkvæmt líkindafallinu eru líkur á k atburðum jafnar
$$p_k = \frac{e^{-\lambda} \lambda^k}{k!}$$.
Þ.e.a.s. líkurnar á útkomunni núll og þar með engum atburði eru $$e^{-\lambda}$$, líkur á einum atburði eru $$e^{-\lambda} \lambda$$, líkur á tveimur atburðum eru $$\frac{1}{2}e^{-\lambda} \lambda^2$$, líkur á þremur atburðum eru $$\frac{1}{6}e^{-\lambda} \lambda^3$$, o.s.frv. Mynstrið er þekkt.
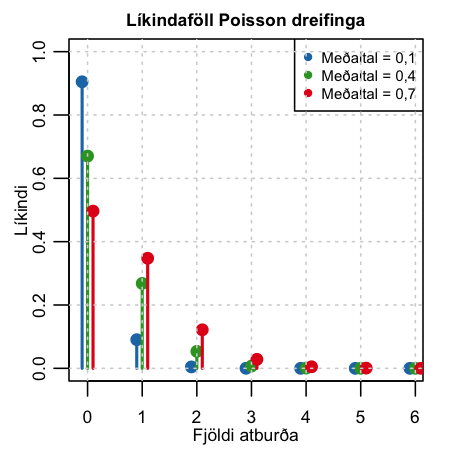
Hugsum okkur dæmi um tryggingafélag, sem flokkar ökumenn þrjá áhættuflokka: lægsta, miðlungs og hæsta. Félagið notar Poisson líkindadreifinguna til þess að tákna tjónatíðni þeirra. Það hefur fundið út að viðskiptavinir í lægsta áhættuflokki valdi að jafnaði 0,1 tjóni á ári pr. ökumann en 0,4 tjón á ári pr. ökumann í miðlungs áhættuflokki og 0,7 tjón að jafnaði í þeim hæsta. Með því að setja stuðlana inn í jöfnurnar fyrir ofan má finna líkindi á fjölda tjóna, sem ökumaður í hverjum flokki veldur. Niðurstaðan er sýnd í meðfylgjandi töflu og líkindafallið er sýnt á myndinni til hægri.
| Fjöldi | Áhættuflokkur | ||
|---|---|---|---|
| tjóna | Lægsti, $$\lambda=0,1$$ | Miðlungs, $$\lambda=0,4$$ | Hæsti, $$\lambda=0,7$$ |
| 0 | 0.905 | 0.670 | 0.497 |
| 1 | 0.090 | 0.268 | 0.348 |
| 2 | 0.005 | 0.054 | 0.122 |
| 3 | <0.001 | 0.007 | 0.028 |