Það komst í fréttirnar í vikunni þegar þremur konum var bjargað úr helli. Í viðtali við Reykjavík síðdegis á Bylgjunni af því tilefni sagði Árni B. Stefánsson, augnlæknir og landskunnur hellakönnuður:

Það er regla hjá hellamönnum að fara aldrei í helli nema með þrjú ljós með sér. … Af því að aðalljósið gæti klikkað og varaljósið gæti klikkað. En það er mjög ólíklegt að þriðja ljósið fari líka. Það er bara líkindareikningur.

Í framhaldinu ræddu útvarspmennirnir svo um búnað, aðstæður í hellaferðum og hverju fljótt göngumenn þreytast í hellum svo eitthvað sé nefnt. Spurningunni um það til hve mikilla bóta það er að bera aukaljós með sér er enn ósvarað.

Uppbygging og áreiðanleiki kerfa

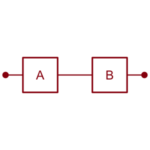
Í greiningu á áreiðanleika þarf að skoða hvern hluta kerfis og uppbyggingu þess. Með raðtengingu kerfishluta er átt við að kerfið virki ef og aðeins ef allir hlutar þess virka. Kerfið á myndinni til hægri er sett saman úr tveimur kerfishlutum, A og B. Það mun aðeins virka á meðan báðir hlutar þess eru í lagi. Þegar annað hvort A eða B bilar þá stoppar kerfið.

Ef við lýsum líftíma hvors hvors kerfishluta um sig með slembibreytunum $$X_A$$ og $$X_B$$ þá er líftími alls kerfisins jafn þeim hluta sem endist skemur, $$R = \min (X_A,X_B)$$.

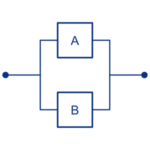
Það er talað um hliðtengt kerfi ef það virkar á meðan einhver hluti þess virkar. Kerfið á myndinni til vinstri er einnig sett samsett úr tveimur hlutum, A og B. Þessari framsetningu er ætlað að tákna að kerfið mun virka á meðan annar hvor hluti þess virkar. Þegar báðir hafa bilað þá hættir kerfið að virka.

Eins og í fyrra dæminu er líftíma hlutanna lýst með slembibreytunum $$X_A$$ og $$X_B$$. Í hliðtengdu kerfi er líftími kerfisins jafn líftíma þess hluta sem dugir lengst, $$S = \max (X_A,X_B)$$.

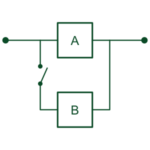
Þriðja uppsetningin lýsir kerfi, sem notar A sem aðalkerfi og B er til vara. Í einfaldaðri uppsetningu gerum við ráð fyrir að varakerfið bili ekki á meðan aðalkerfið er í gangi. Táknmyndunum er ætlað að lýsa því að þegar aðalkerfið bilar mun varakerfið taka yfir. Þegar varakerfið bilar þá stoppar kerfið.

Líftími alls kerfisins er jafn summu líftíma hvors hluta um sig, $$T = X_A + X_B$$.

Hve mörg vasaljós?

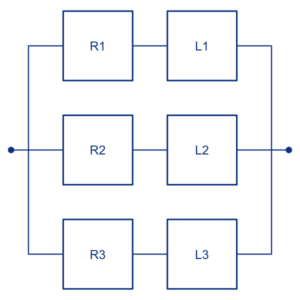
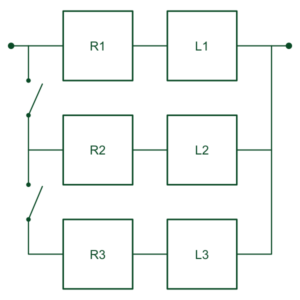
Gerum ráð fyrir að vasaljós hafi eina rafhlöðu og eina ljósaperu, sem við táknum með bókstöfunum R og L í raðtengdu kerfi. Bæði rafhlaðan og ljósaperan þurfa að vera í lagi svo að vasaljósið lýsi. Gerum svo ráð fyrir að hellakönnuðirnir noti þrjú vasaljós í tveimur ólíkum uppsetningum.

Ef þrír hellakönnuðir nota hver sitt vasaljós getum við táknað kerfið eins og sýnt er á bláu myndinni til vinstri. Við gerum ráð fyrir því að ef ljós eins hellakönnuðar bilar þá sé hann studdur áfram af öðrum í hópnum. Svo lengi sem a.m.k. eitt ljós er í lagi geta hellakönnuðirnir haldið för sinni áfram. Köllum þetta kerfi 1.

Ef hellakönnuðir nota eitt aðalljós en bera tvö önnur með sér til vara þá getum við táknað kerfið eins og sýnt er á grænu myndinni hérna til hægri. Þegar aðalljósið bilar er gripið til fyrra varaljóssins. Þegar þegar það bilar er seinna varaljósið notað. Þetta er kerfi 2.

Líftími metinn með hermun

Til þess að meta ábatann af því að fjölga vasaljósum notum hermum við mögulegar útkomur og skoðum dreifingarnar. Gerum ráð fyrir að líftími rafhlaða lúti normaldreifingu með meðaltal 5 klukkustundir og staðalfrávik hálfa klukkustund. Látum líftíma ljósapera lúta veldisdreifingu með meðaltal 10 klukkustundir.

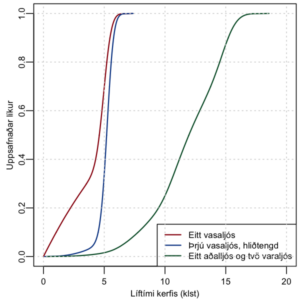
Niðurstöður hermunar sýna að eitt vasaljós dugir að meðaltali í 3,9 klst. og þrjú hliðtengd vasaljós í kerfi 1 að meðaltali í 5,1 klst. Líftími kerfis 2 með eitt aðalljós og tvö til vara dugar er að meðaltali í 11,8 klst. Það er u.þ.b. þrefaldur líftími þegar aðeins eitt ljós er notað.

Sér í lagi höfum við áhuga á lágum útkomum af því að það kemur göngumönnum í koll þegar ljósin bila. Í 5% prósent tilfella er líftími eins vasaljóss styttri en hálf klukkustund. Líftími kerfis nr. 1 er í 5% tilfella styttri en 4,1 klst. og 6,5 klst. með kerfi 2.