Af og til berast fréttir og frásagnir af flökti á verðbréfa- eða gjaldeyrismörkum. Stundum verður tíðindamönnum á orði að flökt hafi lækkað eða að það hafi hækkað. Þá er jafnvel bryddað upp á því að slá mælikvarða á flöktið og að það mælist núna fimmtán eða fimmtíu prósent. En hvað þýðir það?
Flökt (volatility) er mælikvarði á sveiflur í verði verðbréfs eða gengi gjaldmiðils. Þegar óvissa ríkir á fjármálamörkuðum og umrót geysar eru verðbreytingar tíðari og meiri og flökt mælist hærra. Í rólegra árferði mælst flökt lægra. Flökt er ekki beinn mælikvarði á virði verðbréfs en óbeint getur það haft áhrif á verð þess. Mikið flökt kann þannig að draga úr fýsileika þess að eiga tiltekið verðbréf svo að fjárfestar halda að sér höndum. Það kann þannig að draga úr verðhækkunum eða leiða til lækkunar. Aftur á móti er flökt einn af þeim þáttum, sem beinlínis ráða verðlagningu afleiða á undirliggjandi verðbréf eða gjaldmiðlakross. Að því verður kannski vikið síðar.
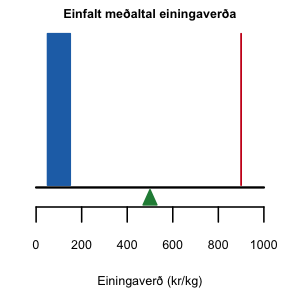
Einfalt er að reikna ávöxtun sem hlutfallsbreytingu á verði bréfs eða gjaldmiðlakross frá upphafsdegi til lokadags. Ávöxtun má líka t.d. reikna sem meðaltal hlutfallsbreytingar verðs pr. viðskiptadag yfir lengra tímabil. Til þess að bera ekki saman epli og appelsínur ef verðathuganir eru með mismunandi tíðni er hægt að staðla framsetninguna og miða við fasta tímalengd, yfirleitt ársávöxtun eða ávöxtun á ársgrunni. Ávöxtun er þannig fyrstu gráðu (first order) tölfræðimæling á breytingu á verði verðbréfs eða gengi gjaldmiðils.
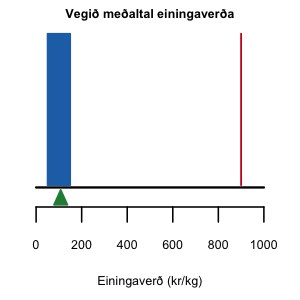
Á sama hátt er flökt annarar gráðu (second order) tölfræðimæling á verðbreytingum verðbréfs eða gengi gjaldmiðils. Flökt er mælt sem staðalfrávik hlutfallsbreytingar á verði, t.d. milli daga, vikna eða mánaða. Til að staðla mælieininguna á sama hátt og fyrr er yfirleitt miðað við flökt á ársgrunni eða ársflökt (annual volatility). Yfirleitt er ekki verið að flækja frásögnina um of og bara talað um flökt, sem kann á móti að þykja óljóst. Í afleiðuviðskiptum er einnig talað um fólgið flökt (implied volatility). Það er ekki eiginleg mæling á flökti heldur það flökt sem verðlagning afurðar endurspeglar.
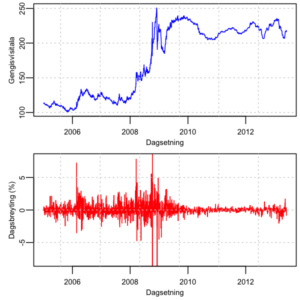
Myndin hérna til hægri sýnir gengisvísitölu íslensku krónunnar nokkur síðustu ár. Gögnin eru fengin frá Seðlanka Íslands. Efra ritið sýnir gildi vísitölunnar en það neðra sýnir dagsbreytingar vísitölunnar. Í útreikningum sem þessum notum við mismunaröð af lógariþma verðsins frá einum tímapunkti til annars. Fyrir litlar verðbreytingar mismunur lógariþmaraðarinnar nokkurn vegin jafnt hlutfallsbreytingu verðsins frá einum degi til annars skv. hefðbundnum prósentuútreikningi.
Fimm sinnum árið 2008 voru dagsbreytingar yfir 8 prósentustig til hækkunar eða lækkunar sem eru klippt ofan eða neðn af myndritinu. Af útslaginu á neðri myndinni má sjá að tíðni stærri útslaga jókst eftir því sem leið á árið 2005 og á árinu 2006 voru allsnarpar breytingar þegar gengi krónunnar lækkaði. Eftir það lækkaði flöktið aftur. Í aðdraganda bankahrunsins jókst flöktið en eðlilega dró úr sveiflunum þegar gjaldeyrishöftum var komið á. Frá ársbyrjun 2012 hefur hefur flöktið heldur aukist.
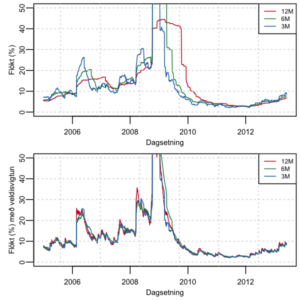
Á myndinni til vinstri hefur flökt (ársflökt) verið reiknað með nokkrum ólíkum aðferðum út frá dagsbreytingum, sem sýndar voru á fyrri mynd. Á efri myndinni eru notaðar þrjár aðferðir hlaupandi glugga með jafnt vægi. Rauði ferillinn lýsir reiknuðu flökti út frá dagsbreytingum næstliðins árs og öll sýni hafa jafnt vægi. Með græna ferlinum hefur glugginn verið styttur niður í 6 mánuði og augljóst að áhrif snarpra hreyfinga vara skemur. Blái ferillinn notar þriggja mánaða tímabil. Of stór gluggi og jafnt vægi getur þannig ýkt áhrif flökts lengur en raunverulegur órói varir á markaði.
Á neðri myndinni er flökt reiknað miðað við sömu gluggastærðir en sýnum er gefið ólíkt vægi. Breyting frá fyrri viðskiptadegi hefur mest vægi en en elstu sýnin vega minnst (veldisvigtun). Miklar breytingar á gengisvísitölu leiða til yfirskots samanborið við aðferð með jöfnu vægi allra sýna. Ferlarnr sýna nokkuð jafna niðurstöðu óháð gluggalengd. Samkvæmt myndunum mælist flökt íslensku krónunnar nú um 8% eftir því hvaða aðferð og gluggastærð beitt er við útreikningana.