Í gær kom út nýtt eintak Fjármála, vefrits Fjármálaeftirlitsins. Meðal efnis að þessu sinni er umfjöllun síðuhöfundar um áhrif nýrra líftaflna á skuldbindingar lífeyrissjóða. Þá er grein um fyrirhugaðar breytingar á löggjöf um vátryggingamarkaði eftir Sigurð Frey Jónatansson, tryggingastærðfræðing. Frétt Fjármálaeftirlitsins um útgáfuna má finna hér.
Félag íslenskra tryggingastærðfræðinga boðar til opins fundar miðvikudaginn 14. október nk. frá kl. 8:30 til 10:00. Fundurinn fer fram í húsakynnum Arion banka í Borgartúni 19. Sjá nánari umfjöllun á vef Félags íslenskra tryggingastærðfræðinga.
Fundurinn er öllum opinn og aðgangur er ókeypis.
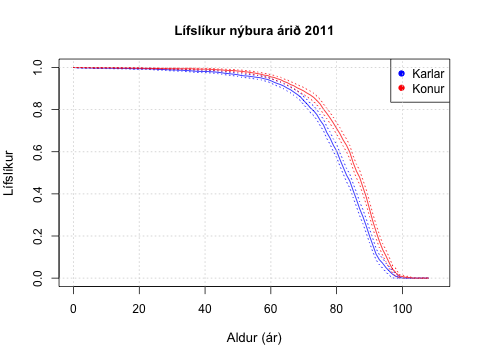
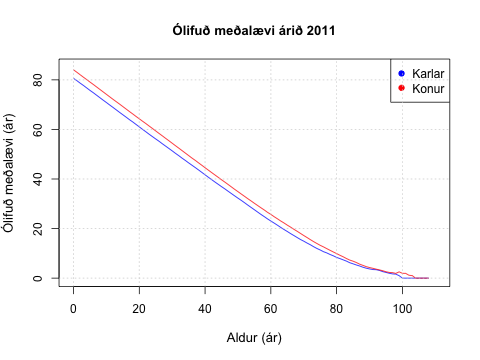
Samkvæmt grein Wikipedia er velgengni í teningaspilinu Yathzee háð leikni eða hæfileikum á þremur sviðum; heppni, kunnáttu í líkindaaðferðum og herkænsku. Ekki er öllum gefið að verða heppnari, ef heppni getur talist til hæfileika á annað borð. En taki menn leikinn alvarlega er mikilvægt að hafa leikáætlun og gott að byggja hana líkindum. Það er gott að hafa það í huga núna í upphafi sumars vilji menn slá vinum og ættingjum ref fyrir rass í sumarbústöðum og á mannamótum á næstunni.
Leikurinn þarfnast ekki útskýringar. Í klassískri útfærslu eru umferðirnar spilaðar í beinni röð og þá ljúka leikmenn næsta lið á leikspjaldinu í hverri umferð. Í öðrum útfærslum er leyfilegt að velja eftir hverja umferð inn á hvaða lið stigum er ráðstafað. Umferðin Áhætta er næst síðasti liðurinn á leikspjaldinu og þar keppast leikmenn við að hámarka stigin sín í þremur köstum. Eftir fyrsta og annað kastið velur leikmaður hvaða teningum hann vill halda en öðrum er kastað aftur. En hvaða tölum á að halda?
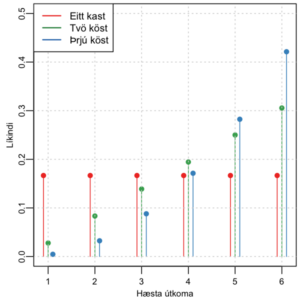
Líkindaþéttifall hæstu úkoma í einu, tveimur og þremur köstum.
Myndin hér til hægri sýnir líkindaþéttifall hæstu útkomu þegar teningi er kastað. Rauðu súlurnar tákna líkindi á útkomu í einu kasti. Með fullkomnum teningi eru líkur á sérhverri útkomu jafnar, þ.e. 1/6 eða 0.16667. Líkurnar má einnig tákna í prósentum sem 16,667%.
Þegar teningi er kastað tvisvar sinnum og hærri útkoman er valin aukast líkur á háum útkomum. Grænu súlurnar tákna líkur á hæstu útkomu þegar teningi er kastað tvisvar. Líkurnar á að hærri úkoman í tveimur köstum sé sex er $$1 – (\frac{5}{6})^2 = 0.30556$$. Líkurnar á að hærri útkoman í tveimur köstum sé jöfn einum er $$(\frac{1}{6})^2 = 0.02778$$. Til þess þurfum við að fá ás í báðum köstum.
Á sama hátt er hægt að reikna líkur á hæstu útkomu í þremur köstum, sem táknaðar eru með bláu súlunum. Líkurnar á því að hæsta úkoman í þremur köstum sé sex er 0,42130. Líkurnar á að fá ás í öllum köstum og að hæsta útkoman sé þar með einn eru 0,00463.
Þá kemur aftur að leikáætluninni sem var nefnd í upphafi. Hvaða teningum ætti að halda eftir fyrsta kastið? Gildir öðru eftir annað kastið?
Væntigildi útkoma í hverju kasti er reiknað sem meðaltal mögulegra útkoma. Áður en tengingunum er kastað í fyrstu umferð er væntigildi útkomu fyrir sérhvern tening
$$1\cdot\frac{1}{216}+2\cdot\frac{7}{216}+3\cdot\frac{19}{216}+4\cdot\frac{37}{216}+5\cdot\frac{61}{216}+6\cdot\frac{91}{216}=\frac{1071}{216}=4,9583$$.
Eftir fyrsta kastið eru tvær umferðir eftir og væntigildi útkomu fyrir sérhvern tening er reiknað á sama hátt og áður
$$1\cdot\frac{1}{36}+2\cdot\frac{3}{36}+3\cdot\frac{5}{36}+4\cdot\frac{7}{36}+5\cdot\frac{9}{36}+6\cdot\frac{11}{36}=\frac{21}{6}=4,4722$$.
Þegar eitt kast er eftir eru jafnar líkur á öllum hliðum og væntigildið er því
$$1\cdot\frac{1}{6}+2\cdot\frac{1}{6}+3\cdot\frac{1}{6}+4\cdot\frac{1}{6}+5\cdot\frac{1}{6}+6\cdot\frac{1}{6}=\frac{21}{6}=3,5$$.
Nú er leikáætlunin valin þannig að væntigildi sé hámarkað í hverri umferð. Niðurstaðan er að eftir fyrstu umferðina ætti leikmaður að halda fimmum og sexum vegna þess að þær eru hærri en 4,4722, sem er vænt útkoma ef kastað væri aftur. Eftir aðra umferð ætti að halda fjörkum, fimmum og sexum vegna þess að vænt útkoma í þriðja kastinu er 3,5.
Rétt er að nefna að aðstæður hverju sinni kunna að réttlæta aukna áhættusækni. Ef vinna þarf upp naumt forskot keppinautar má setja þröskuldinn ofar, jafnvel þótt að lækki væntigildi mögulegra útkoma í leiknum.
Þeir sem þekkja til R forritunarmálsins vita að það er eftir ýmsu því tengdu að slæðast á netinu. Síðustu árin hefur verið veldisvöxtur í fjölda pakka, sem notendur geta nálgast frítt. Bæði byrjendur og lengra komnir geta haft gagn og gaman af þessari kynningu Jim Guszcza á notkun R í ýmsum viðfangsefnum tengdum tryggingastærðfræði. Það er vel þess virði að horfa á.
Ég kynntist Jim síðasta vetur þegar hann var prófessor í tryggingastærðfræði við University of Wisconsin-Madison þar sem ég tók námskeið hjá honum. Þar byrjaði ég að nota R í fyrsta sinn sem bætti miklu við hagnýtingu námsefnisins.
Those who are familiar with the R programming language know the near endless resources available online. In recent years, the number of free libraries has grown exponentially. Beginners and advanced programmers can enjoy and learn from this presentation given by Jim Guszcza on actuarial applications using R. I guarantee it is worth watching.
It was my privilege to sit Jim’s class on loss models during my studies at the University of Wisconsin-Madison last year. His extensive use of R added a lot to the practical aspects of the course material.
httpv://www.youtube.com/watch?v=yWexhOmkVKU
Forsenda þess að verðleggja líftengdar tryggingarafurðir, hvort heldur er líftryggingar eða lífeyriseign, er að meta lífslíkur einstaklings, sem í hlut á. Það er því við hæfi að fyrsta efnilega innleggið í þessu bloggi fjalli um mat á lífslíkum.
Til þess að meta lífslíkur er stuðst við upplýsingar um mannfjölda og andlát. Í mannfjöldatöflum er alla jafna skráð hve mörg heil ár einstaklingar lifa. Út frá upplýsingum um mannfjölda og andlát fyrir hvert aldursbil má reikna lífslíkur hvers aldursárs. Að því gefnu er svo hægt að reikna ólifaða meðalævi, þ.e. fjölda ára sem einstaklingur getur vænst þess að lifa að því gefnu að hann sé á lífi við tiltekinn aldur.
Myndin hér fyrir neðan sýnir lífslíkur nýbura á Íslandi m.v. dánartíðni árið 2011 skv. tölum um mannfjölda og andlát, sem Hagstofa Íslands skráir. Heilu línurnar tákna lífslíkurnar en brotastrikin tákna 95% öryggismörk. Myndin byggir aðeins á tölum eins árs. Í litlum þjóðfélögum má nota upplýsingar yfir lengra tímabil til þess að minnka óvissubilið.
Samkvæmt myndinni teljast 99,4% líkur á því að nýfætt sveinbarn nái 20 ára aldri og 99,7% líkur á því að stúlkubarn nái sama aldri. Það eru 3,2% líkur á því að karlmaður deyji fyrir fimmtugt en 1,5% að það sama hendi konu.
Í samanburði á milli þjóða er venja að bera saman vænta ævilengd nýbura en á sama hátt má reikna vænta ólifaða meðalævi m.v. hvert aldursár. Þannig má vænta að nýfætt sveinbarn nái um 80 ára aldri og stúlkubörn um 84 ára aldri.
Myndin hér að ofan sýnir væntingar um ólifaða meðalævi fyrir öll aldursár. Nái karlmaður 80 ára aldri er væntur árafjöldi, sem hann á eftir ólifaða, u.þ.b. 8 ár. Kona, sem nær sama aldri, á um 10 ár eftir ólifuð að meðaltali.
Þetta er fyrsta færslan í nýju bloggi um tryggingastærðfræði. Það er ásetningur að fjalla um fræðin á bak við trygginga- og lífeyrismál og flétta saman við málefni líðandi stundar þar sem við á. Ef síðan verður til þess að auka áhuga einhvers á faginu eða varpa upp nýjum vinklum í umræðunni þá er tilganginum náð.
Ég lauk nýverið námi við tryggingastærðfræðideild University of Wisconsin í Madison, Wisconsin í Bandaríkjunum. Áður lauk ég meistaraprófi í rafmagns- og tölvuverkfræði frá Háskóla Íslands.
Jón Ævar Pálmason